CUDA 已經熾手可熱一段時間了,好像程式經過CUDA加持,效能都加了不少。可惜CUDA不能加在人身上,不然原本一百公尺跑個15秒,CUDA上身也許可以跑個9秒9。
我也觀望一段時間了,想看看CUDA和OpenCL誰勝出,再來學。但等著等著,火都快熄了。上網查了一下,看到有一本新書,"CUDA By Example",在台灣買要新台幣1800元,去 Amazon.com 查了一下,含運費(最一般的運費,號稱要40天才能到)才美金不到五十元。心想也不急,就訂了。十天左右,就拿到書。翻了前幾章,有點基本概念,剛好有一筆資料要處理,雖然已經先用傳統方式解決了,心裡覺得可以用CUDA試試,就動手來寫第一支CUDA程式了。
資料來源是模擬的結果,想要看 Iso-surface。但我一開始只得到一筆200×300的網格資料,如下圖:
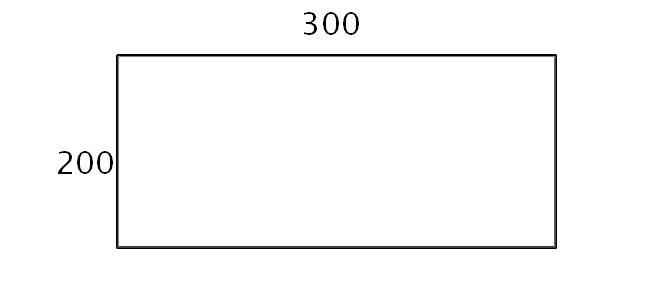
那是對一個圓柱形流場做模擬,所以雖然只給一片資料,但因為是對稱資料,得先由那筆資料算出整個圓柱體的資料,示意圖如下:
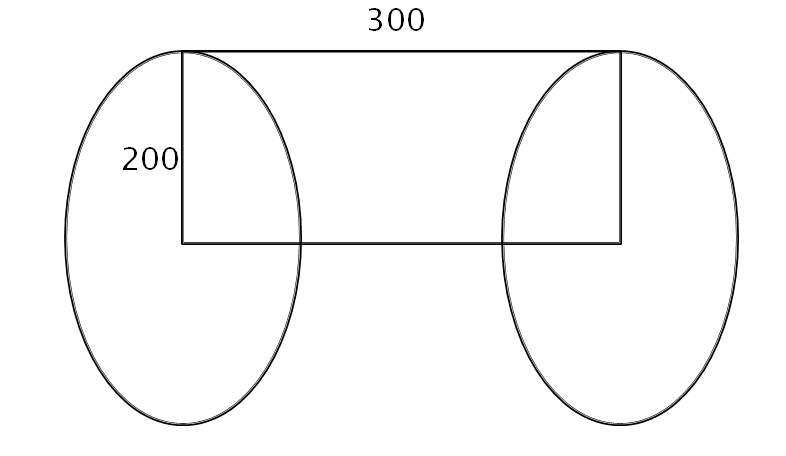
想法很簡單,就是建立一個三維的volume data 把這圓柱包住。資料的格式,是200×300,所以每讀進200的點,就可以產生出一個 slice 的資料(如下圖)
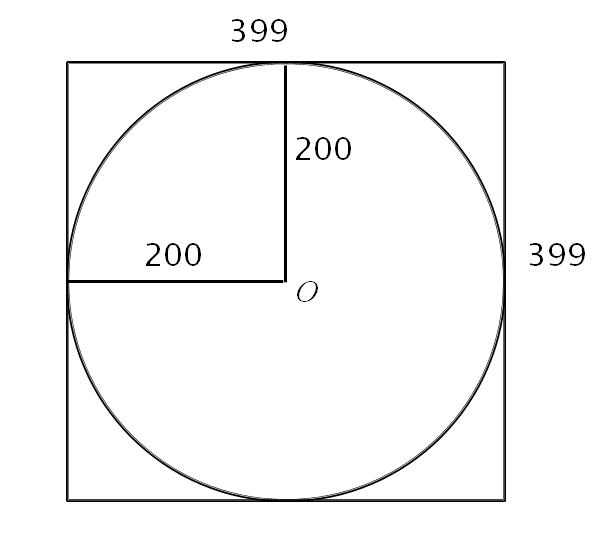
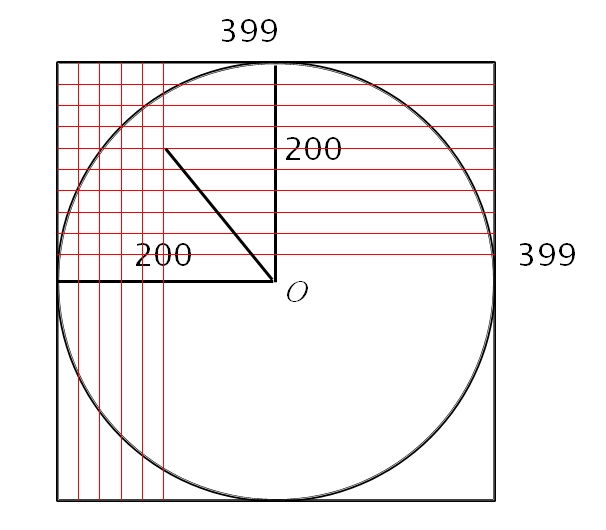
如上圖右,這 slice 的每個點,都可以由和原點的距離來決定。Pseudo Code 如下:
CreateOneSlice(float *line, int r){ for (i=0 to 2*r-1) for (j=0 to 2*r-1) { dist = Dist(O, Pij) Vij = Interpolation(dist, line) }}
如此重覆300次,就完成了整個Volume data了。
CUDA Implemenataion
因為一面在看 CUDA 的書,就想到,在單一 Slice 上的每個點,都是獨立的,可以分別用一個 thread 來計算,很適合平行計算,就決定用 CUDA 來試試。
void CreateOneSliceGPU(int attr_index, FILE *outf, float *dev_Slice){ int sliceDim = g_DIMY*2-1; if(g_Slice==0) g_Slice = new float[sliceDim*sliceDim]; double t1, t2; t1 = wallclock(); cudaMemcpy(dev_fYData, g_fYData, g_DIMY*sizeof(float), cudaMemcpyHostToDevice); dim3 grid((sliceDim block_dim-1)/block_dim, (sliceDim block_dim-1)/block_dim); dim3 threads(block_dim, block_dim); slice_kernel<<<grid, threads>>>(g_DIMY, dev_fYData, dev_Slice); cudaMemcpy(g_Slice, dev_Slice, sliceDim*sliceDim*sizeof(float), cudaMemcpyDeviceToHost); t2 = wallclock(); TIME_USED = (t2-t1); fwrite(g_Slice, sizeof(float), sliceDim*sliceDim, outf)}
dev_fYData 就儲存200個點的值,做為 linear-interpolation用。每讀入200點資料就可以輸出一張Slice。dev_Slice 已事先用 cudaMalloc 宣告一塊記憶體了。
Kernel code 如下 (因為用HTML語法空格太多, 所以用圖檔):

結果:
後來真的實作,是用兩筆資料,150×300 和 300×600 兩組。block_dim 我有做不同的測試,以下是其中一組結果(block_dim=10):
CPU vs. GPU
150×300 : 1086 ms vs. 195 ms
300×600 : 9030 ms vs. 1276 ms
運算時間的確縮短不少。
後記:
1. 我後來還有再把 g_fYData 放在 constant memory 裡,時間還會再縮短一些。
2. 這支程式,其實是一個多月前寫的。這幾個星期,又再試了 APSP (All Pair Shortest Path)的 CUDA code,有空再放上來(FW 方法,和 blocked 加速方法)。不過在這裡放程式碼實在不方便,我再想想要如何解決。
3. 本次結果的幾張 snapshots:
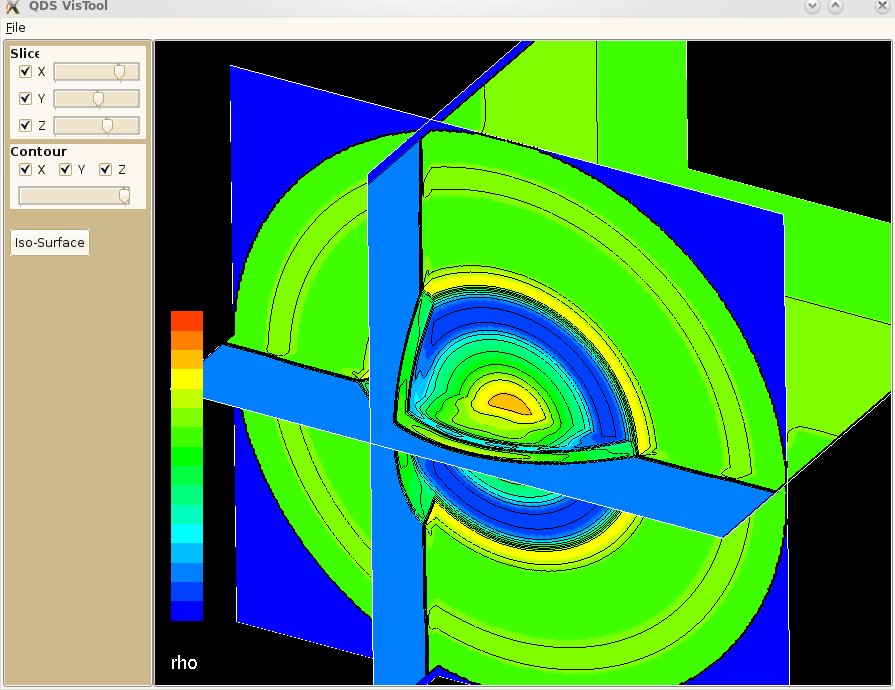
圓柱的三個方向切面,加上 contour lines
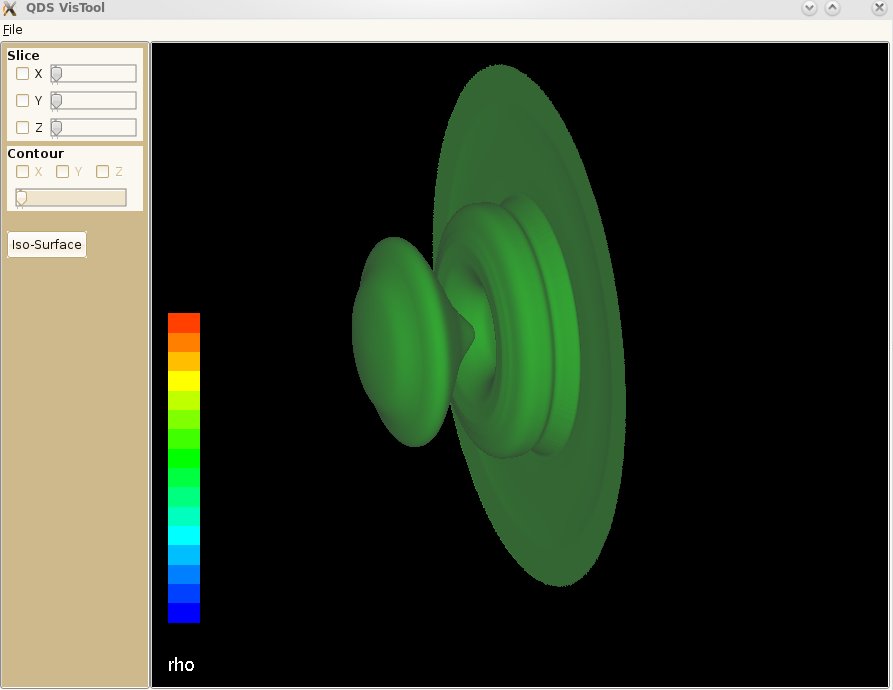
Iso-surfaces
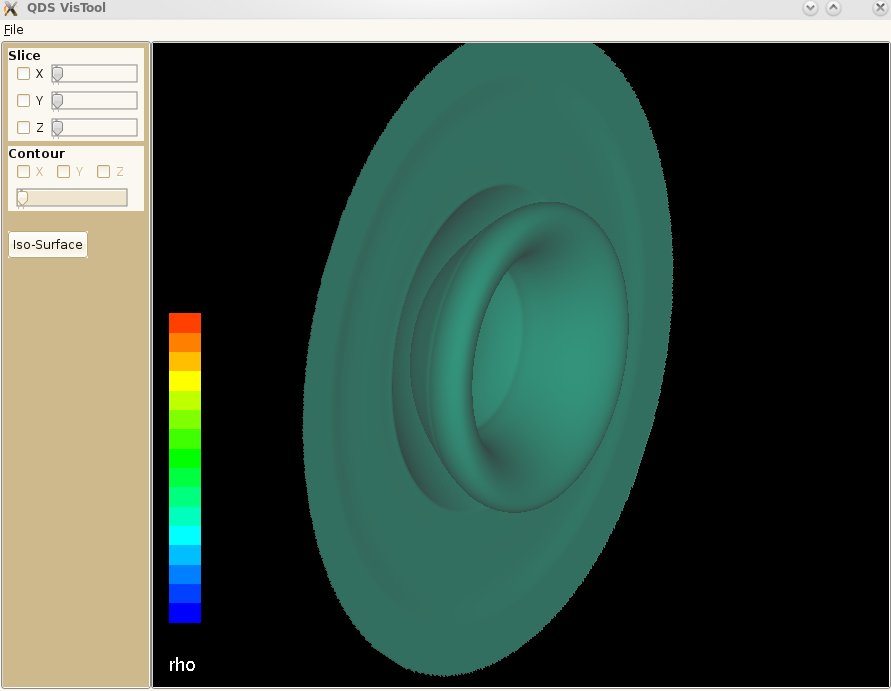
另一組 Iso-surfaces
本文同時發佈於 a-small-place.blogspot.com/2010/11/cuda.html

